u32 Operations

In this section we describe semantics and AIR constraints of operations over u32 values (i.e., 32-bit unsigned integers) as they are implemented in Miden VM.

Range checks

Most operations described below require some number of 16-bit range checks (i.e., verifying that the value of a field element is smaller than $2^{16}$). The number of required range checks varies between $2$ and $4$, depending on the operation. However, to simplify the constraint system, we force each relevant operation to consume exactly $4$ range checks.

To perform these range checks, the prover puts the values to be range-checked into helper registers $h_0, ..., h_3$, and then updates the range checker bus column $b_{range}$ according to the LogUp construction described in the range checker documentation, using multiplicity $1$ for each value.

This operation is enforced via the following constraint. Note that since constraints cannot include divisions, the actual constraint which is enforced will be expressed equivalently with all denominators multiplied through, resulting in a constraint of degree 5.

$$b_{range}' = b_{range} - \frac{1}{(\alpha - h_0)} - \frac{1}{(\alpha - h_1)} - \frac{1}{(\alpha - h_2)} - \frac{1}{(\alpha - h_3)} \text{ | degree} = 5$$

The above is just a partial constraint as it does not show the range checker's part of the constraint, which adds the required values into the bus column. It also omits the selector flag which is used to turn this constraint on only when executing relevant operations.

Checking element validity

Another primitive which is required by most of the operations described below is checking whether four 16-bit values form a valid field element. Assume $t_0$, $t_1$, $t_2$, and $t_3$ are known to be 16-bit values, and we want to verify that $2^{48} \cdot t_3 + 2^{32} \cdot t_2 + 2^{16} \cdot t_1 + t_0$ is a valid field element.

For simplicity, let's denote:

$$v_{hi} = 2^{16} \cdot t_3 + t_2 v_{lo} = 2^{16} \cdot t_1 + t_0$$

We can then impose the following constraint to verify element validity:

$$\left(1 - m \cdot (2^{32} - 1 - v_{hi})\right) \cdot v_{lo} = 0 \text{ | degree} = 3$$

Where $m$ is a value set non-deterministically by the prover.

The above constraint should hold only if either of the following hold:

• $v_{lo} = 0$
• $v_{hi} \ne 2^{32} - 1$

To satisfy the latter equation, the prover needs to set $m = (2^{32} - 1 - v_{hi})^{-1}$, which is possible only when $v_{hi} \ne 2^{32} - 1$.

This constraint is sufficient because modulus $2^{64} - 2^{32} + 1$ in binary representation is 32 ones, followed by 31 zeros, followed by a single one:

$$1111111111111111111111111111111100000000000000000000000000000001$$

This implies that the largest possible 64-bit value encoding a valid field element would be 32 ones, followed by 32 zeros:

$$1111111111111111111111111111111100000000000000000000000000000000$$

Thus, for a 64-bit value to encode a valid field element, either the lower 32 bits must be all zeros, or the upper 32 bits must not be all ones (which is $2^{32} - 1$).

U32SPLIT

Assume $a$ is the element at the top of the stack. The U32SPLIT operation computes $(b,c) \leftarrow a$, where $b$ contains the lower 32 bits of $a$, and $c$ contains the upper 32 bits of $a$. The diagram below illustrates this graphically.

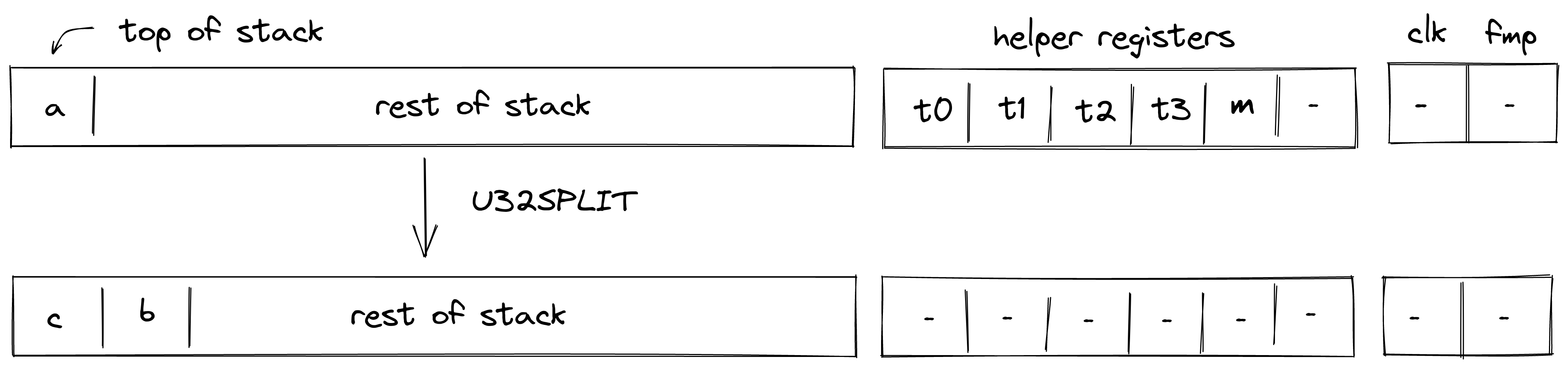
To facilitate this operation, the prover sets values in $h_0, ..., h_3$ to 16-bit limbs of $a$ with $h_0$ being the least significant limb. Thus, stack transition for this operation must satisfy the following constraints:

$$s_{0} = 2^{48} \cdot h_3 + 2^{32} \cdot h_2 + 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$ $$s_{1}' = 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$ $$s_{0}' = 2^{16} \cdot h_3 + h_2 \text{ | degree} = 1$$

In addition to the above constraints, we also need to verify that values in $h_0, ..., h_3$ are smaller than $2^{16}$, which we can do using 16-bit range checks as described previously. Also, we need to make sure that values in $h_0, ..., h_3$, when combined, form a valid field element, which we can do by putting a nondeterministic value $m$ into helper register $h_4$ and using the technique described here.

The effect of this operation on the rest of the stack is:

• Right shift starting from position $1$.

U32ASSERT2

Assume $a$ and $b$ are the elements at the top of the stack. The U32ASSERT2 verifies that both $a$ and $b$ are smaller than $2^{32}$. The diagram below illustrates this graphically.

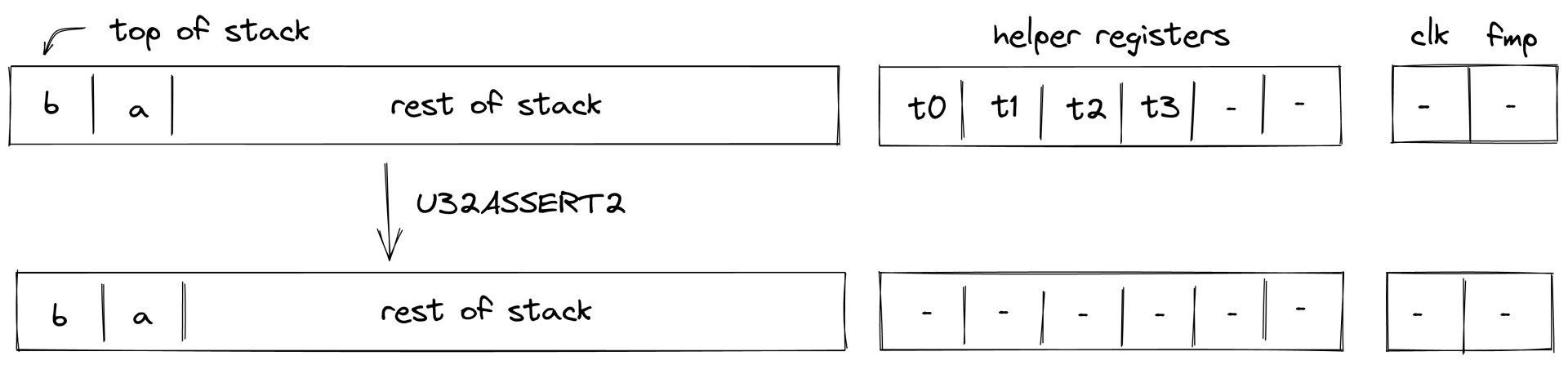
To facilitate this operation, the prover sets values in $h_0$ and $h_1$ to low and high 16-bit limbs of $a$, and values in $h_2$ and $h_3$ to to low and high 16-bit limbs of $b$. Thus, stack transition for this operation must satisfy the following constraints:

$$s_0' = 2^{16} \cdot h_3 + h_2 \text{ | degree} = 1$$ $$s_1' = 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$

In addition to the above constraints, we also need to verify that values in $h_0, ..., h_3$ are smaller than $2^{16}$, which we can do using 16-bit range checks as described previously.

The effect of this operation on the rest of the stack is:

• No change starting from position $0$ - i.e., the state of the stack does not change.

U32ADD

Assume $a$ and $b$ are the values at the top of the stack which are known to be smaller than $2^{32}$. The U32ADD operation computes $(c,d) \leftarrow a + b$, where $c$ contains the low 32-bits of the result, and $d$ is the carry bit. The diagram below illustrates this graphically.

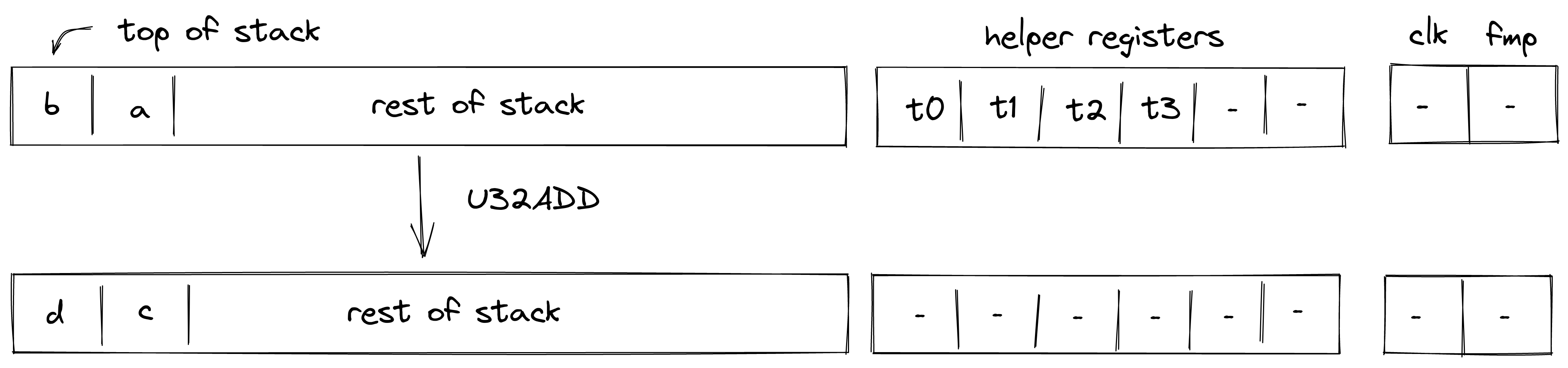
To facilitate this operation, the prover sets values in $h_0$, $h_1$, and $h_2$ to 16-bit limbs of $a+b$ with $h_0$ being the least significant limb. Value in $h_3$ is set to $0$. Thus, stack transition for this operation must satisfy the following constraints:

$$s_0 + s_1 = 2^{32} \cdot h_2 + 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$ $$s_0' = h_2 \text{ | degree} = 1$$ $$s_1' = 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$

In addition to the above constraints, we also need to verify that values in $h_0, ..., h_3$ are smaller than $2^{16}$, which we can do using 16-bit range checks as described previously.

The effect of this operation on the rest of the stack is:

• No change starting from position $2$.

U32ADD3

Assume $a$, $b$, $c$ are the values at the top of the stack which are known to be smaller than $2^{32}$. The U32ADD3 operation computes $(d, e) \leftarrow a + b + c$, where $c$ and $d$ contains the low and the high 32-bits of the result respectively. The diagram below illustrates this graphically.

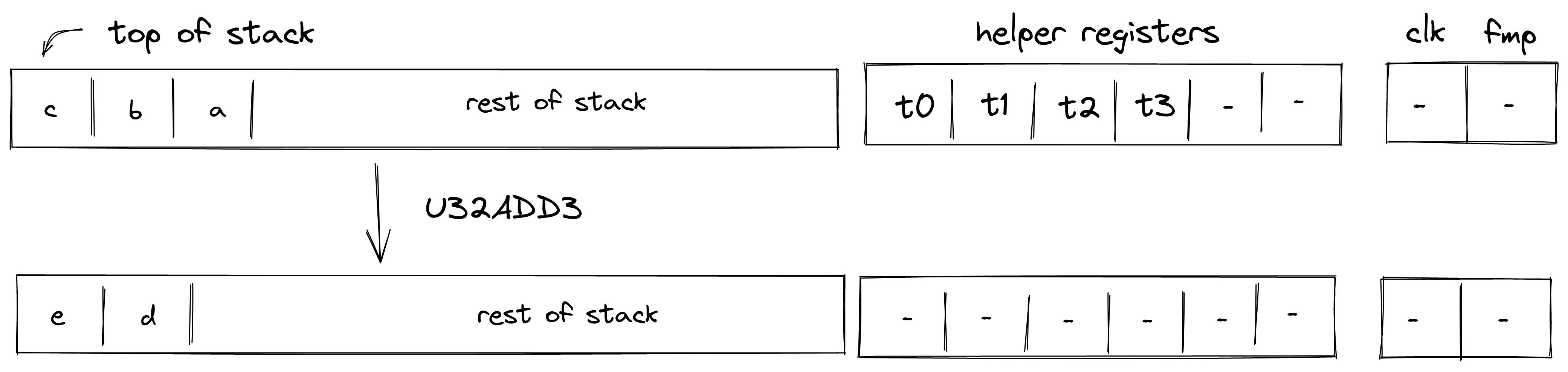
To facilitate this operation, the prover sets values in $h_0$, $h_1$, and $h_2$ to 16-bit limbs of $a+b+c$ with $h_0$ being the least significant limb. Value in $h_3$ is set to $0$. Thus, stack transition for this operation must satisfy the following constraints:

$$s_0 + s_1 + s_2 = 2^{32} \cdot h_2 + 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$ $$s_0' = h_2 \text{ | degree} = 1$$ $$s_1' = 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$

In addition to the above constraints, we also need to verify that values in $h_0, ..., h_3$ are smaller than $2^{16}$, which we can do using 16-bit range checks as described previously.

The effect of this operation on the rest of the stack is:

• Left shift starting from position $3$.

U32SUB

Assume $a$ and $b$ are the values at the top of the stack which are known to be smaller than $2^{32}$. The U32SUB operation computes $(c, d) \leftarrow a - b$, where $c$ contains the 32-bit result in two's complement, and $d$ is the borrow bit. The diagram below illustrates this graphically.

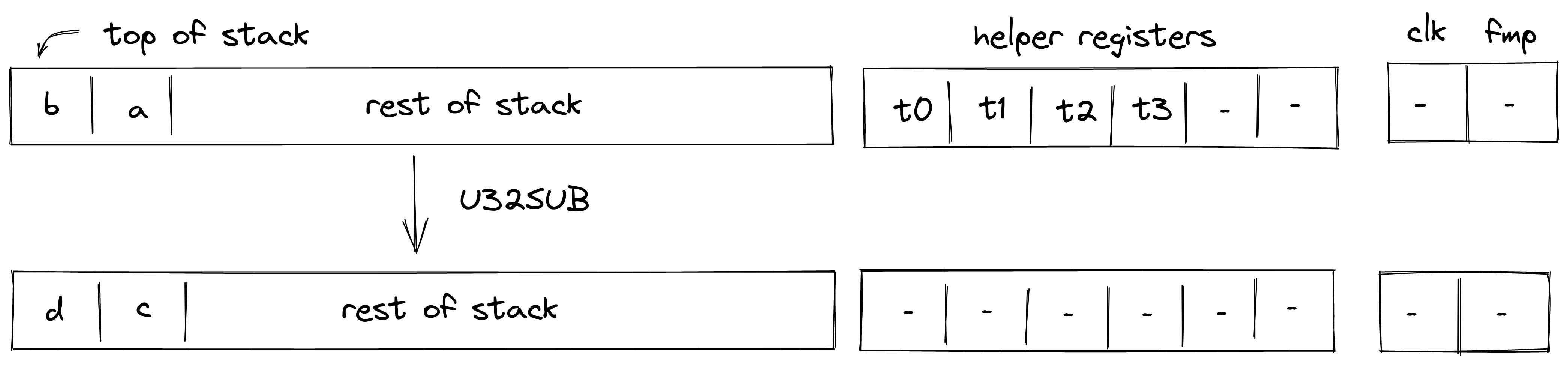
To facilitate this operation, the prover sets values in $h_0$ and $h_1$ to the low and the high 16-bit limbs of $a-b$ respectively. Values in $h_2$ and $h_3$ are set to $0$. Thus, stack transition for this operation must satisfy the following constraints:

$$s_1 = s_0 + s_1' + 2^{32} \cdot s_0' \text{ | degree} = 1$$ $$s_0'^2 - s_0' = 0 \text{ | degree} = 2$$ $$s_1' = 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$

In addition to the above constraints, we also need to verify that values in $h_0, ..., h_3$ are smaller than $2^{16}$, which we can do using 16-bit range checks as described previously.

The effect of this operation on the rest of the stack is:

• No change starting from position $2$.

U32MUL

Assume $a$ and $b$ are the values at the top of the stack which are known to be smaller than $2^{32}$. The U32MUL operation computes $(c, d) \leftarrow a \cdot b$, where $c$ and $d$ contain the low and the high 32-bits of the result respectively. The diagram below illustrates this graphically.

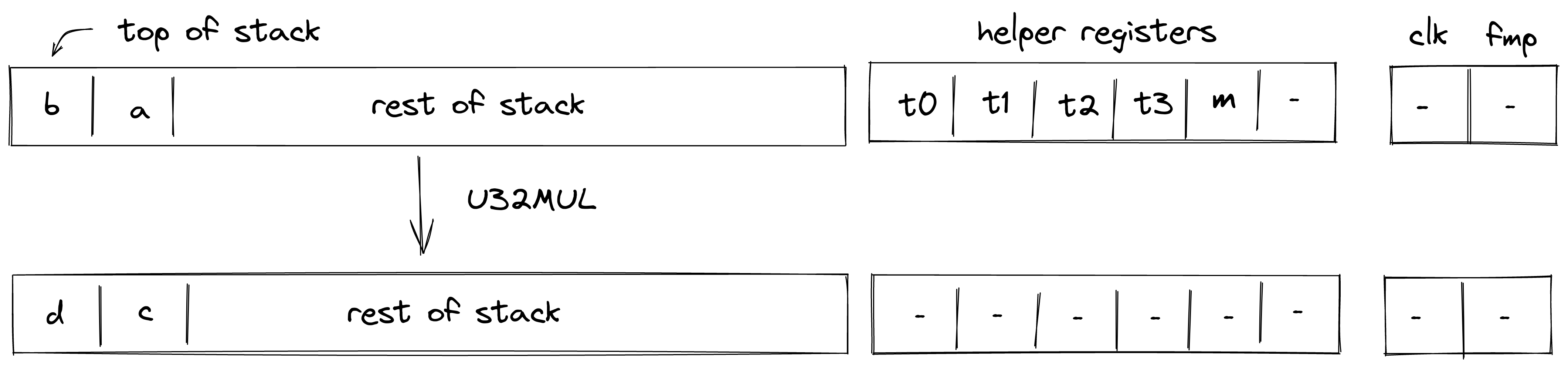
To facilitate this operation, the prover sets values in $h_0, ..., h_3$ to 16-bit limbs of $a \cdot b$ with $h_0$ being the least significant limb. Thus, stack transition for this operation must satisfy the following constraints:

$$s_0 \cdot s_1 = 2^{48} \cdot h_3 + 2^{32} \cdot h_2 + 2^{16} \cdot h_1 + h_0 \text{ | degree} = 2$$ $$s_1' = 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$ $$s_0' = 2^{16} \cdot h_3 + h_2 \text{ | degree} = 1$$

In addition to the above constraints, we also need to verify that values in $h_0, ..., h_3$ are smaller than $2^{16}$, which we can do using 16-bit range checks as described previously. Also, we need to make sure that values in $h_0, ..., h_3$, when combined, form a valid field element, which we can do by putting a nondeterministic value $m$ into helper register $h_4$ and using the technique described here.

The effect of this operation on the rest of the stack is:

• No change starting from position $2$.

U32MADD

Assume $a$, $b$, $c$ are the values at the top of the stack which are known to be smaller than $2^{32}$. The U32MADD operation computes $(d, e) \leftarrow a +b \cdot c$, where $c$ and $d$ contains the low and the high 32-bits of $a + b \cdot c$. The diagram below illustrates this graphically.

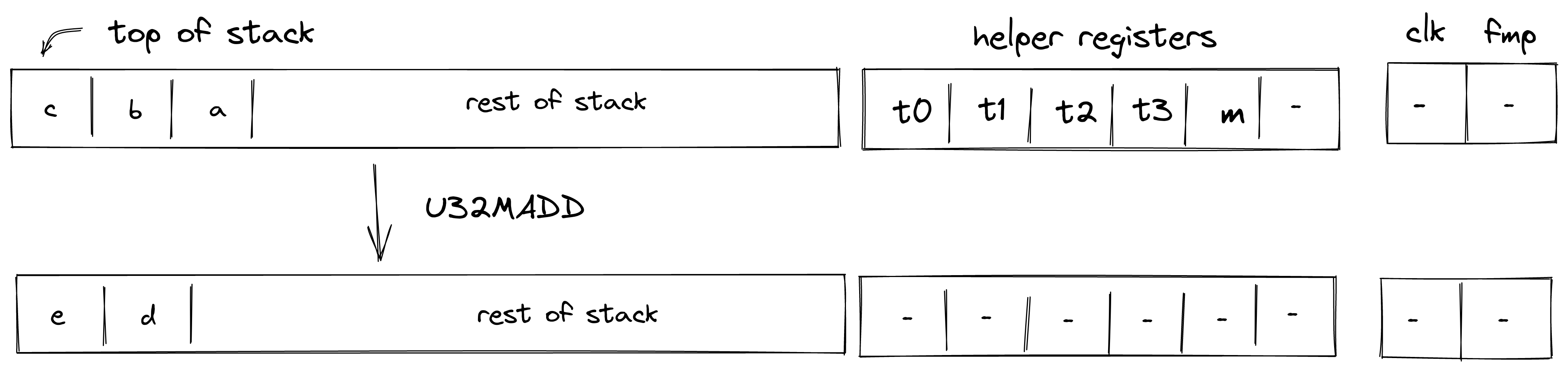
To facilitate this operation, the prover sets values in $h_0, ..., h_3$ to 16-bit limbs of $a + b \cdot c$ with $h_0$ being the least significant limb. Thus, stack transition for this operation must satisfy the following constraints:

$$s_0 \cdot s_1 + s_2 = 2^{48} \cdot h_3 + 2^{32} \cdot h_2 + 2^{16} \cdot h_1 + h_0 \text{ | degree} = 2$$ $$s_1' = 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$ $$s_0' = 2^{16} \cdot h_3 + h_2 \text{ | degree} = 1$$

In addition to the above constraints, we also need to verify that values in $h_0, ..., h_3$ are smaller than $2^{16}$, which we can do using 16-bit range checks as described previously. Also, we need to make sure that values in $h_0, ..., h_3$, when combined, form a valid field element, which we can do by putting a nondeterministic value $m$ into helper register $h_4$ and using the technique described here.

Note: that the above constraints guarantee the correctness of the operation iff $a + b \cdot c$ cannot overflow field modules (which is the case for the field with modulus $2^{64} - 2^{32} + 1$).

The effect of this operation on the rest of the stack is:

• Left shift starting from position $3$.

U32DIV

Assume $a$ and $b$ are the values at the top of the stack which are known to be smaller than $2^{32}$. The U32DIV operation computes $(c, d) \leftarrow a / b$, where $c$ contains the quotient and $d$ contains the remainder. The diagram below illustrates this graphically.

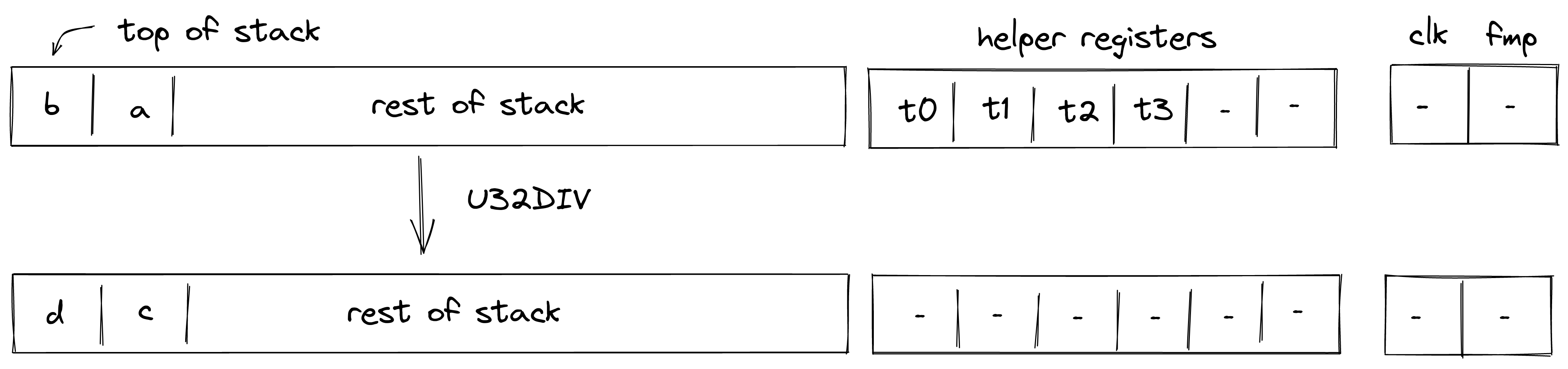
To facilitate this operation, the prover sets values in $h_0$ and $h_1$ to 16-bit limbs of $a - c$, and values in $h_2$ and $h_3$ to 16-bit limbs of $b - d - 1$. Thus, stack transition for this operation must satisfy the following constraints:

$$s_1 = s_0 \cdot s_1' + s_0' \text{ | degree} = 2$$ $$s_1 - s_1' = 2^{16} \cdot h_1 + h_0 \text{ | degree} = 1$$ $$s_0 - s_0' - 1= 2^{16} \cdot h_2 + h_3 \text{ | degree} = 1$$

The second constraint enforces that $s_1' \leq s_1$, while the third constraint enforces that $s_0' < s_0$.

The effect of this operation on the rest of the stack is:

• No change starting from position $2$.

U32AND

Assume $a$ and $b$ are the values at the top of the stack. The U32AND operation computes $c \leftarrow (a \land b)$, where $c$ is the result of performing a bitwise AND on $a$ and $b$. The diagram below illustrates this graphically.

To facilitate this operation, we will need to make a request to the chiplet bus $b_{chip}$ by dividing its current value by the value representing bitwise operation request. This can be enforced with the following constraint:

$$b_{chip}' \cdot \left(\alpha_0 + \alpha_1 \cdot op_{u32and} + \alpha_2 \cdot s_0 + \alpha_3 \cdot s_1 + \alpha_4 \cdot s_0' \right) = b_{chip} \text{ | degree} = 2$$

In the above, $op_{u32and}$ is the unique operation label of the bitwise AND operation.

Note: unlike for many other u32 operations, bitwise AND operation does not assume that the values at the top of the stack are smaller than $2^{32}$. This is because the lookup will fail for any inputs which are not 32-bit integers.

The effect of this operation on the rest of the stack is:

• Left shift starting from position $2$.

U32XOR

Assume $a$ and $b$ are the values at the top of the stack. The U32XOR operation computes $c \leftarrow (a \oplus b)$, where $c$ is the result of performing a bitwise XOR on $a$ and $b$. The diagram below illustrates this graphically.

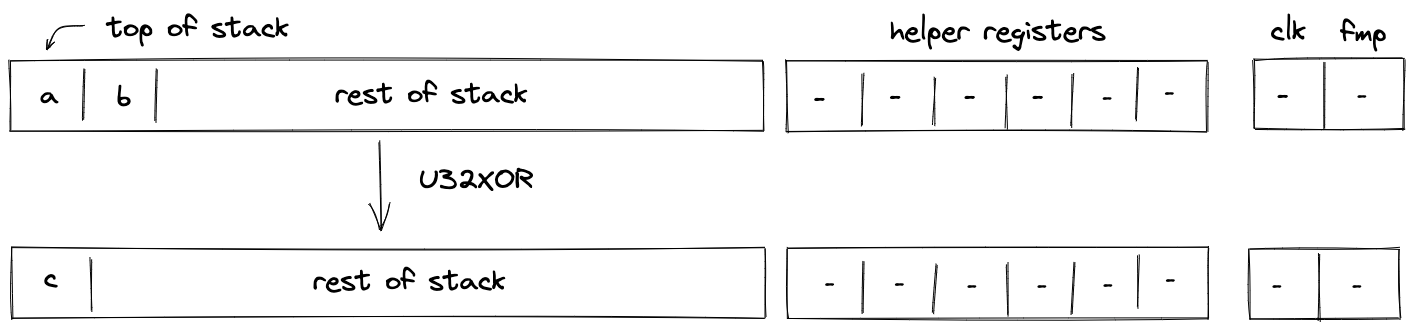
To facilitate this operation, we will need to make a request to the chiplet bus $b_{chip}$ by dividing its current value by the value representing bitwise operation request. This can be enforced with the following constraint:

$$b_{chip}' \cdot \left(\alpha_0 + \alpha_1 \cdot op_{u32xor} + \alpha_2 \cdot s_0 + \alpha_3 \cdot s_1 + \alpha_4 \cdot s_0' \right) = b_{chip} \text{ | degree} = 2$$

In the above, $op_{u32xor}$ is the unique operation label of the bitwise XOR operation.

Note: unlike for many other u32 operations, bitwise XOR operation does not assume that the values at the top of the stack are smaller than $2^{32}$. This is because the lookup will fail for any inputs which are not 32-bit integers.

The effect of this operation on the rest of the stack is:

• Left shift starting from position $2$.